Page 4 - 2018송도수학

04 SONGDO HIGH SCHOOL

다각형의 넓이 쉽게 구하기 / 픽의 정리

평소에 수학 공부를 열심히 하였다면 헤론의 공식을 알 수 있 의 공식뿐만 아니라 더 알리고자 하는 정리는 픽의 정리이다.

다. 헤론의 공식이란 길이가 각 a, b, c인 선분으로 이루어진 삼 픽의 정리란 오스트리아의 게오르그 픽 이라는 수학자가

각형이 있을 때, 면적을 S라고 하면, 1899년 격자 모양의 평면 위에 놓여진 다각형의 넓이를 구하는

S= 가 성립하고, 이때의 s는 방법을 제시하면서 시작되었다. 픽의 정리를 이용해보기 위해서

를 의미한다. 이는 삼각형의 넓이를 쉽게 구하는 기초적인 공 는 격자점이 핵심이 되는데, 선이 겹치지 않는 다각형의 경우 다

식이다. 하지만 대부분의 사람들은 헤론의 공식은 알지라도 사 각형 내부의 격자점을 I개, 다각형의 둘레에 격자점의 개수를 B

각형의 넓이를 쉽게 구하는 공식은 모르고 있다. 사각형의 넓 라고 하였을 경우 넓이 “S = I + - 1” 라는 값이 나오게 된

이를 쉽게 구하는 공식으로는 브라마굽타의 공식이 있다. 헤론 다. 대부분의 다각형 같은 경우 넓이를 구하는 방식이 존재한다.

의 공식과 유사하며 원에 내접하는 사각형의 네 변의 길이를 알 하지만 불규칙한 도형 같은 경우 넓이를 구하기 쉽지가 않기에

고 있을 때 그 사각형의 면적을 구하는 공식이다. 원에 내접하 이러한 곳에 픽의 정리가 많이 사용된다.

는 사각형의 각 선분의 길이가 a, b, c, d일 때, 사각형의 넓이 사람들의 주목을 받게 된 것도 50년이 되지 않는데, 1969년

S는 가 성립한다. 이 때의 s는 슈타인하우스의 책에 실리면서 사람들의 이목을 집중시켰다. 그

를 의미한다. 그러나 헤론의 공식이나 브라마굽타 러면 두 문제를 픽의 정리를 이용해 쉽게 풀어보겠다.

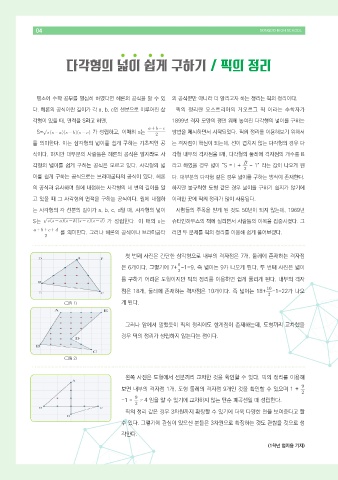
첫 번째 사진은 간단한 삼각형으로 내부의 격자점은 7개, 둘레에 존재하는 격자점

은 6개이다. 그렇기에 7+ -1=9, 즉 넓이는 9가 나오게 된다. 두 번째 사진은 넓이

를 구하기 어려운 도형이지만 픽의 정리를 이용하면 쉽게 풀리게 된다. 내부의 격자

점은 18개, 둘레에 존재하는 격자점은 10개이다. 즉 넓이는 18+ -1=22가 나오

(그림 1) 게 된다.

그러나 앞에서 말했듯이 픽의 정리에도 한계점이 존재하는데, 도형끼리 교차했을

경우 픽의 정리가 성립하지 않는다는 점이다.

(그림 2)

왼쪽 사진은 도형에서 선분끼리 교차한 것을 확인할 수 있다. 픽의 정리를 이용해

보면 내부의 격자점 1개, 도형 둘레의 격자점 9개인 것을 확인할 수 있으며 1 +

-1 = 4 임을 알 수 있기에 교차하지 않는 단순 폐곡선일 때 성립한다.

픽의 정리 같은 경우 3차원까지 확장할 수 있기에 더욱 다양한 면을 보여준다고 할

수 있다. 그렇기에 관심이 있으신 분들은 3차원으로 확장하는 것도 괜찮을 것으로 생

각한다.

(1학년 엄지용 기자)